作者:李士昱、孙冬凯、梁程远
雪球期权是一种新兴的结构较为复杂的期权产品,雪球期权的定价的准确性和速度直接影响交易双方的收益和风险水平。目前我司雪球期权定价采用的是基于C++程序实现蒙特卡罗vwin 的方法。本文为解决基于C++的传统定价程序带来的处理时间长、延迟高、处理速率低的问题,提出并实现了一种基于FPGA的并行流水线计算处理设计,能够完成对雪球期权的定价功能,并使用HLS开发模式对设计进行了实现。通过对比测试,相对于通用处理器与C++软件实现的定价方式可获得约17.83倍的性能提升。
引 言
普通欧式期权通常可以使用Black-Scholes模型进行定价,雪球期权在欧式期权的基础上引入的观察日和敲入敲出的概念,使得其定价无法运用类似模型获得一个确定的期望价格,因此需要使用蒙特卡罗方法进行模拟。蒙特卡罗方法是一种对过程随机抽样的程序,我们可以通过随机采样得到近似的结果,其拥有采样越多,越近似最优解的特点。蒙特卡罗方法广泛应用于科学计算的各种领域。传统思路是使用通用微处理器(CPU)进行蒙特卡罗模拟,在这种情况下通常需要通过提高处理器单核性能或者多线程方式提高模拟速度,也有使用GPU等专用计算处理器的尝试。然而近年来,随着摩尔定律渐渐失效,处理器单核性能提升逐渐放缓,而人们对计算量的需求随着大数据、人工智能等技术的发展却越来越大,因此对传统体系结构的变革需求变得越来越迫切。
随着FPGA技术的不断发展,利用FPGA进行硬件加速已经逐步成为一个新的趋势。一方面相比通用架构,FPGA能够根据功能需求进行定制,获得更好的性能和功耗;另一方面相比开发专用硬件,FPGA的开发周期更短,成本更低,其可重构特性使得能够根据算法变化快速进行更新迭代。此外,Xilinx公司推出的HLS和苹果等公司推出的OpenCL等开发标准使得开发者能够使用高级语言如C或C++进行硬件开发工作,进一步降低了开发门槛,提升了开发效率[1]。
本文设计并使用Xilinx公司提供的HLS开发方式,利用C++语言实现了定价实现了基于FPGA的雪球期权定价程序,并作为动态链接库,通过Java本地接口JNI提供调用,作为dubbo服务整合到了场外衍生品OMS订单管理系统中。
1 雪球期权的定价方法
雪球期权的本质是一种卖出带触发条件的看跌期权。雪球期权属于奇异期权,因此带有奇异期权的障碍概念,“障碍”是指当标的资产价格在特定时间内穿越某一水平该期权才会生效或者失效。“障碍”一般分为敲出和敲入两类。敲出即当标的资产价格达到一个特定的障碍水平时,该期权了结并兑现赔付,若规定时间内标的资产价格没有触及障碍水平,则为一个普通期权。敲入与敲出期权相反,当标的资产价格达到一个特定障碍水平时,该期权才能触发约定赔付机制,若规定时间内标的资产价格没有触及障碍水平,则不触发约定赔付机制。
一个雪球期权的要素表示如下:
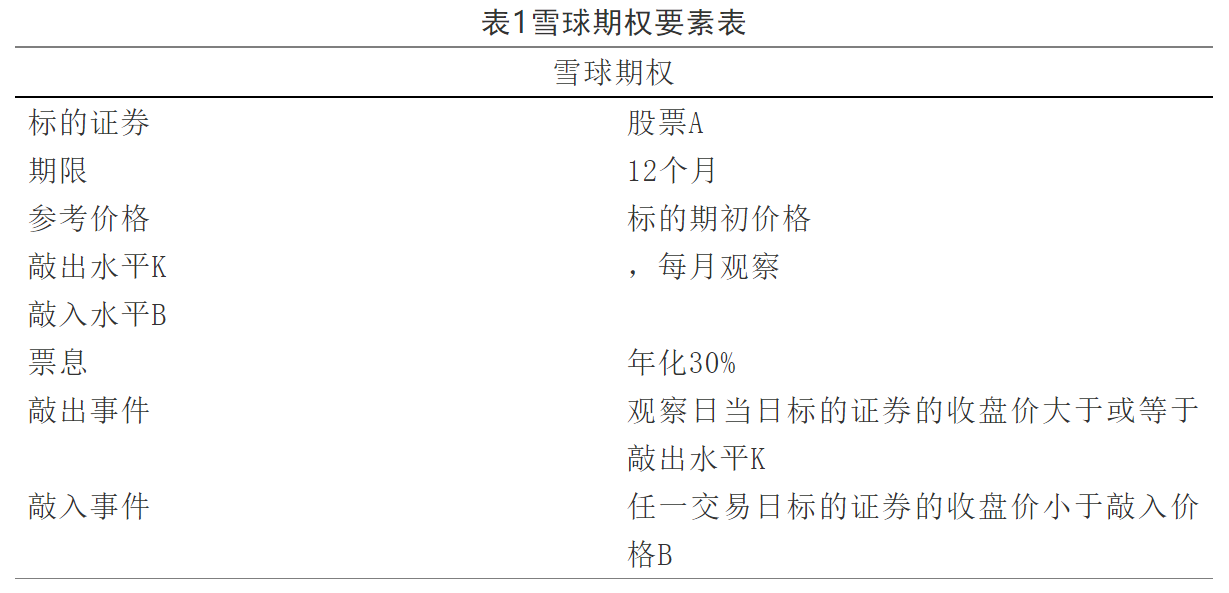
雪球期权存续或结束时可能出现三种情形:
(1)产品发出敲出事件,此时无论是否发生敲入事件,产品将提前结束,客户可获得票息收益,按照产品实际存续期计算。
(2)产品存续期未发生敲出或敲入事件,客户可在产品到期时获得票息收益,按产品期限计算。
(3)产品存续期发生了敲入事件但未发生敲出事件,则客户无票息收益,且可能承担亏损,,如无跌幅则无亏损。
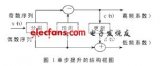
由上述条件可得到雪球期权收益率如图1所示:
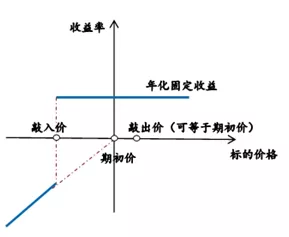
图 1雪球期权收益
由于雪球期权障碍的存在,我们难以直接给出雪球期权的价格模型,因此考虑采用蒙特卡罗方法对作为标的的股票价格进行抽样,根据股票价格和障碍条件确定雪球期权最终收益,将收益折现后得到雪球期权的当前价格。
2 雪球期权定价程序设计
2.1 雪球期权蒙特卡罗定价程序设计
我们以几何布朗运动模型描述风险中性情况下股票价格随时间变化的离散形式如下[2]:
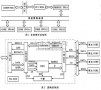
其中为无风险利率 ,为股票波动率,服从标准正态分布。我们需要对该随机过程进行蒙特卡罗模拟,获得标的股票期权存续期内的价格路径。蒙特卡罗模拟程序主要有两个模块,一是生成服从标准正态分布的随机数,二是完成价格计算,进行股票价格路径模拟,并根据模拟结果计算雪球期权价格,由此可得到定价程序流程图如图2所示:

图 2雪球期权定价程序流程图
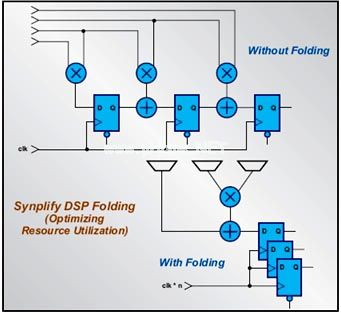
在通用处理器上程序都是串行顺序执行,执行效率不高。本文提出了基于FPGA的解决方案。在处理方式上采用流水线执行,并在路径模拟部分根据硬件资源使用进行一定程度的并发,进一步提高了路径模拟的吞吐量。

图3雪球期权定价在FPGA多并发流水线的执行流程示例
2.2 定价程序开发模式
传统FPGA开发方式通常采用RTL级描述,如使用Verilog或VHDL语言。RTL级开发虽然直接描述硬件的行为,能够获得更加准确、性能更好的电路设计,但是对于软件工程师来说门槛较高,调试优化时间也更长,就好像在用汇编语言进行软件开发一样。为了解决这些问题,Xilinx公司推出了支持高层次综合(High-Level Synthesis)的编译工具,使开发人员能够使用C/C++语言进行FPGA开发,把精力更多集中在算法实现上面,不需要亲自动手进行底层细节的实现,极大提升了开发效率。图4展示了使用RTL设计方法的传统FPGA开发方式、HLS开发方式与其他平台主流设计开发方法的开发时间和理想性能对比。
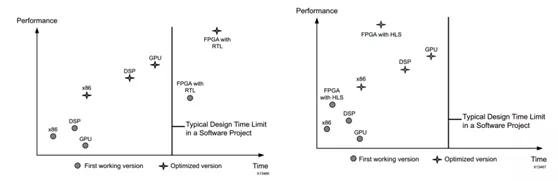
图4不同平台开发方式时间和理想性能对比[3]
总体来说,HLS可以自动完成以下曾经需要手动完成的工作,包括[4]:
(1)HLS自动分析并利用一个算法中潜在的并发性;
(2)HLS自动在需要的路径上插入寄存器,并自动选择最理想的时钟;
(3)HLS自动产生控制数据在一个路径上出入方向的逻辑;
(4)HLS自动完成设计的部分与系统中其他部分的接口;
(5)HLS自动映射数据到储存单位以平衡资源使用与带宽;
(6)HLS自动将程序中计算的部分对应到逻辑单位,在实现等效计算的前提下自动选取最有效的实施方式。
本文采用HLS方式进行雪球期权定价程序的开发,一方面可以降低开发难度,将幂计算、开方计算、浮点数处理等硬件开发难点交由编译器进行处理,提升开发速度,另一方面能够专注于算法实现,从更高层级优化程序的执行效率,提升程序优化效率,在更短时间内获得更高性能提升。
3定价程序实现与优化
3.1 总体设计与实现
雪球定价程序参照Xilinx推荐的层次结构,总体自下至上可以分为三个层次:最下层L1层提供了用于构建内核的低级原语,包括随机数生成器、路径模拟、累加器等模块;中间层由L1层各模块构建,并辅以更高层次层次逻辑控制和计算模块,并以FPGA内核形式提供定价引擎的接口;L3层则将数据传输、与内核相关的资源配置和任务调度的低层细节抽象化,提供了供高级语言或软件可直接调用的接口,通过调用即可完成定价引擎内核的部署和运行。
此外,我们将定价用JNI包装后编译成动态链接库,使用Java微服务进行调用,从而将定价服务云化,进一步为交易人员提供使用便利。图5展示了定价功能的整体架构。
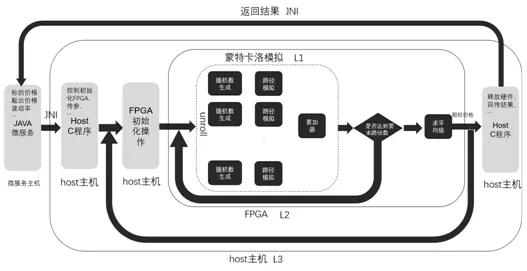
图5FPGA雪球定价程序总体架构设计
3.2 核心模块设计实现与优化
蒙特卡罗模拟主要功能在L1层实现,L1层共分为随机数生成、路径模拟和累加器三个模块。
3.2.1 随机数生成
随机数生成模块要求能够生成符合标准正态分布的随机数,这里我们复用了Xilinx提供的随机数发生器。Xilinx共提供了三种正态分布随机数发生器,分别为MT19937IcnRng、MT2003IcnRng和MT19937BoxMullerNomralRng。第一种使用MT19937随机数,通过逆累计函数变换获得最终结果;第二种使用MT2203随机数,同样为逆累计函数变换获得结果,与第一种不同的是MT2203的周期略短,同时理论上多实例的相关性更弱,随机性也更好一些;第三种是使用MT19937随机数,通过Box-Muller变换得到正态随机数,其优点是性能和资源消耗略小。本文采用MT19937BoxMullerNomralRng随机数发生器来生成随机数。生成的随机数会按序放入一个队列中结构中,供路径模拟模块取用,并通过这一队列将两个模块衔接起来组成一个长流水线。在HLS中这种队列使用hls命名空间的stream类型来表示。
3.2.2 路径模拟
路径模拟是定价程序最重要的模块,也是逻辑最复杂、对总体性能影响最大的模块。在该模块中需要对一条完整的随机过程路径进行模拟,也即模拟标的股票在期权存续期内的价格,并根据价格判断是否触发雪球期权的敲入敲出。
路径中每节点开始首先判断期权是否已经敲出,如敲出则该路径直接结束,如未敲出,则将上一节点价格和随机数计算带入定价公式,算出当前节点股票价格,随后判断是否是观察日和敲入敲出等障碍条件是否满足,并根据结果调整敲入敲出标志,最后判断该路径模拟是否已经结束,如未结束则开始模拟路径中下一个节点,处理流程如图6所示。
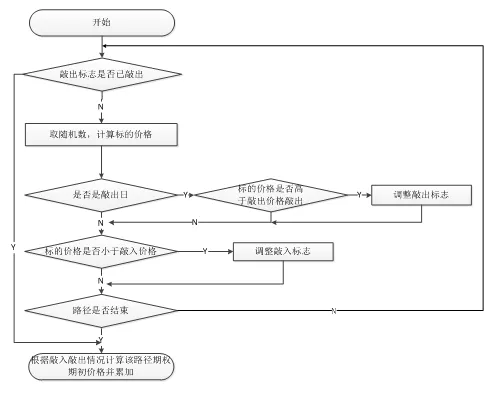
图6路径模拟模块初始处理流程
FPGA的性能优势主要体现在流水线处理和并行两个方面,在HLS开发过程中主要是通过对循环进行流水线处理和展开实现,可以通过加入Pragma提示编译器进行优化工作,如:
for(int i = 0; i
#pragma HLS pipeline II = 1
…
}
其中#pragma HLS pipeline即告诉编译器将该循环按照流水线展开,II为循环起始间隔,即本次循环到下一次循环开始的时钟周期数,本例II=1即告诉编译器我们期望每周期能够启动新的循环迭代,相应的即流水线填满后每周期能够产生一个结果,编译器会根据期望结果进行尝试,实际优化效果未必能够完全实现。
编译器对于能够流水线化循环的结构也有两点要求:一是循环尽量为单层循环且有固定边界,二是如果无法满足单层循环,则尽量在两层循环之间没有逻辑操作且让内层循环拥有固定边界[5]。
回顾路径模拟的处理流程图我们可以发现,循环初始对敲入敲出的判断在CPU顺序执行的情况下能够避免后续无用的循环,但是在FPGA平台则会导致循环无法顺利流水化,因此需要对处理流程进行调整,将敲出结果保存下来留到循环结束再进行处理,从而固定循环边界,使循环能够顺利展开并减少分支损耗。该优化使得循环迭代周期从II=17降至II=5,优化后的处理流程如图7所示:
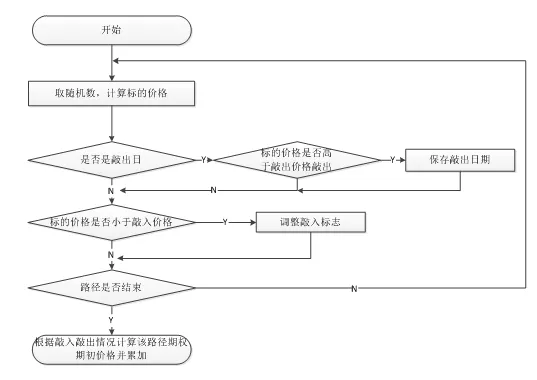
图7优化后的路径模拟处理流程
3.2.3 累加器
累加器模块一方面将各个路径的结果累加并求平均得到最终结果,另一方面也负责随机数生成和路径模拟两个模块的衔接,以及路径模拟的并行展开控制。
由于蒙特卡罗模拟路径各路径间的结果相互独立,因此非常适合并行执行,在HLS中的实现方式也非常简单,如下所示:
for(int i = 0; i
#pragma HLS unroll factor = unrollNum
mcSimulation();//蒙特卡罗模拟函数
}
通过#pragma HLS unroll告知编译器对该循环进行展开并行执行,factor = unrollNum告知编译器并行度,该部分可以省略,如省略则编译器会将循环完全展开。
各路径模拟结果将会暂存至与随机数类似的队列流中,该队列在实例化为硬件后将会是一个RAM结构,其读写口数量和大小编译器会根据代码自动确定,通常为1读口1写口。使用同样RAM结构的C++数据结构还有数组等。当循环充分流水线化且并行展开后,对RAM的读写将会非常频繁,自动生成的RAM读写口数量可能会无法满足我们的需求,造成流水线阻塞。这时候就需要告知编译器所需要的RAM大小和读写口数量,一种方式是直接告知采用的RAM规格,另一种方式是通过将数组或队列拆分。以一个完全拆分即每一个数均采用寄存器存储,深度为64的队列为例,使用HLS的实现写法为:
#pragma HLS stream variable = sumStrm depth =64
#pragma HLS array_partition variable =sunStrm dim = 0
4 测试与分析
4.1 测试环境
FPGA测试平台:Xilinx公司的Alveo U200 FPGA加速卡,该FPGA加速卡被划分为3个内核,本次测试仅测试单核下的资源利用达到极限的性能,XRT运行环境版本为u200_201830_2,在Vitis 2019.2开发环境下完成的开发、综合、验证工作。
对比程序为使用QuantLib库开发的基于蒙特卡罗模拟的雪球期权定价程序,开发语言为C++,运行环境处理器为Intel i7-8700,主频3.2GHz,内存16GB,操作系统为64位Windows 10。
测试方法:在两个平台使用相同期权参数分别运行雪球期权的定价程序,蒙特卡罗路径数为20万条,路径节点数为246个,对应246个交易日。程序循环运行100次,每次对股票波动率进行调整,对比平均运行时间和定价结果误差。期权主要参数如表2所示:
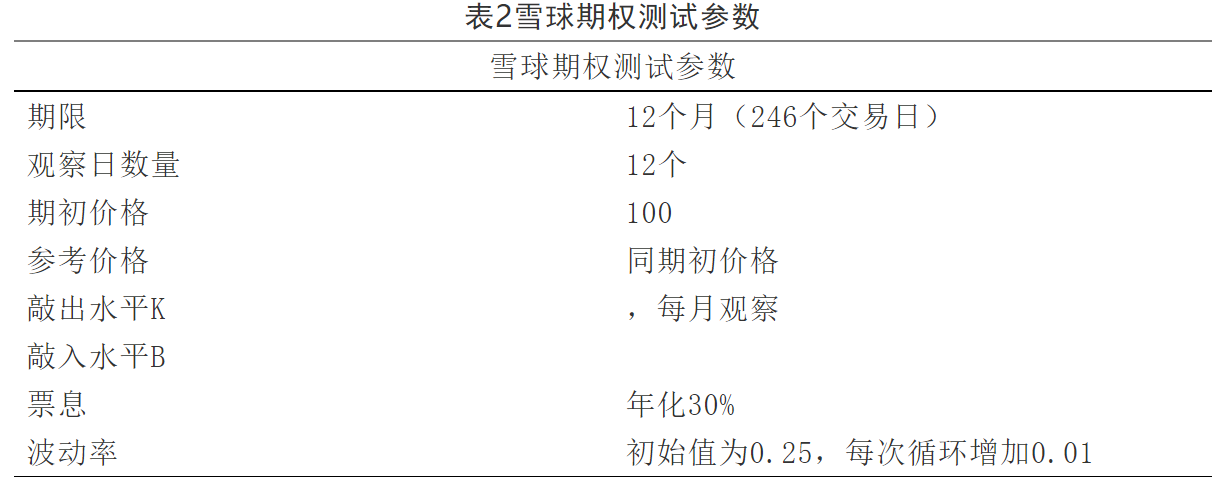
4.2 结果分析
FPGA与C++对比程序定价结果如图8所示,FPGA定价结果相对C++定价结果误差平均值为2.6%,方差为0.0245。与FPGA定价结果相比,C++程序的定价曲线更不平滑,考虑到两边随机数的种子与随机数生成方式均不相同,且蒙特卡罗为对随机过程的抽样近似,可以认为FPGA的定价结果准确,能够满足定价使用要求。
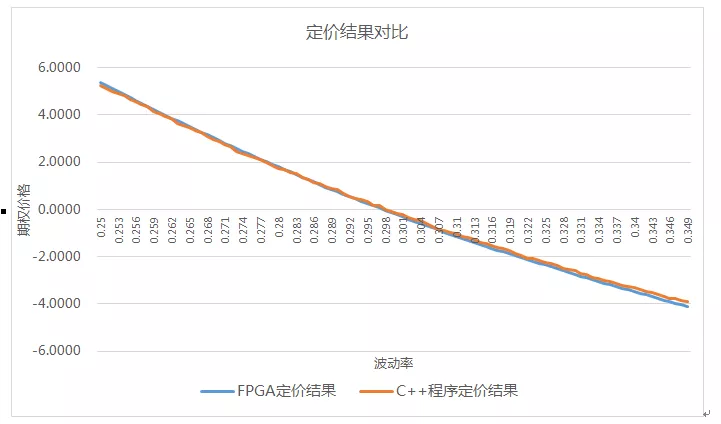
图8雪球期权FPGA定价结果与C++程序定价结果对比
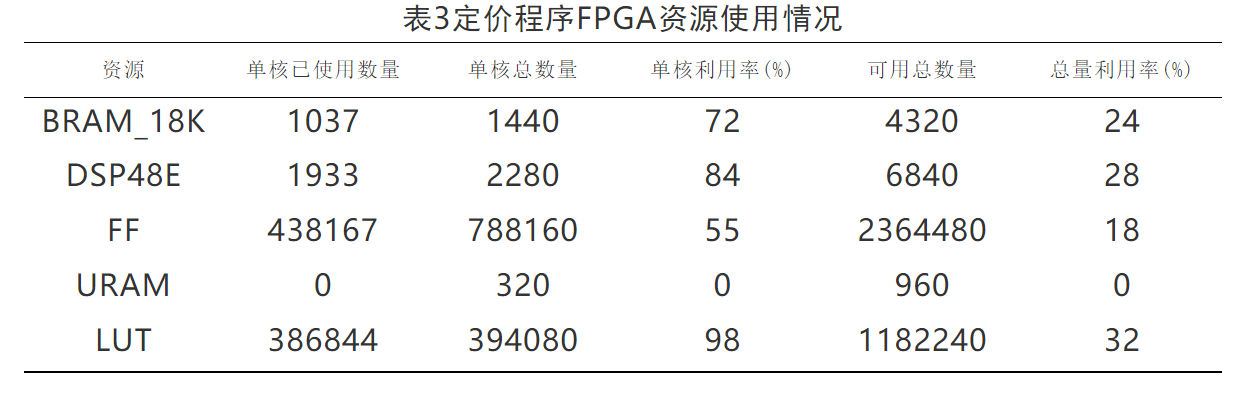
两者执行时间对比,C++程序平均每次定价时间为1153.48ms,FPGA程序平均定价时间为62.75ms,性能提升约为17.38倍。资源利用率如表3所示,其中最高的LUT查找表单核使用率为98%,基本达到单核性能极限。
5 结束语
本文采用流水线并行的设计结构实现了对雪球期权的定价,相比于传统软件的处理方式,本设计在处理时间上显著提高,其性能提升约为17.38倍左右。基于本设计在现有的Alveo U200 FPGA加速卡上使用HLS开发模式构建了雪球期权定价功能,具有稳定性好、延迟低、效率高、处理速率快等特点,取得了良好的测试效果,具有较高的工程实用价值。
审核编辑:郭婷
 德赢Vwin官网
App
德赢Vwin官网
App
























评论